16 buněk
Ve čtyřrozměrné geometrii je šestnáctiúhelník pravidelný konvexní polychoron neboli polytop existující ve čtyřech rozměrech. Je také známý jako hexadekachoron. Je to jeden ze šesti pravidelných konvexních polychorů, které poprvé popsal švýcarský matematik Ludwig Schläfli v polovině 19. století.
Conway ji nazývá ortoplex pro ortantový komplex, stejně jako celou třídu křížových polytopů.
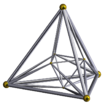
A hexadecachoron
Geometrie
Šestihran je členem rodiny polytopů zvaných křížové polytopy, které existují ve všech dimenzích. Jako takový je jeho duálním polychoronem teserakt (čtyřrozměrná hyperkostka).
Je ohraničen 16 buňkami, které jsou všechny pravidelnými čtyřstěny. Má 32 trojúhelníkových stěn, 24 hran a 8 vrcholů. Těchto 24 hran ohraničuje 6 čtverců ležících v 6 souřadnicových rovinách.
Osm vrcholů hexadekachoronu je (±1, 0, 0, 0), (0, ±1, 0, 0), (0, 0, ±1, 0), (0, 0, 0, 0, ±1). Všechny vrcholy jsou spojeny hranami s výjimkou protilehlých dvojic.
Schläfliho symbol hexadekachoronu je {3,3,4}. Jeho vrcholovým obrazcem je pravidelný osmistěn. V každém vrcholu se setkává 8 čtyřstěnů, 12 trojúhelníků a 6 hran. Jeho hranovým obrazcem je čtverec. Na každé hraně se setkávají 4 čtyřstěny a 4 trojúhelníky.
Existuje forma s nižší symetrií šestnáctiúhelníku, která se nazývá demitesseract nebo 4-demicube, patří do rodiny demihypercube a je reprezentována h{4,3,3} a lze ji nakreslit dvoubarevně se střídajícími se čtyřstěnnými buňkami.
Obrázky
· 
Stereografická projekce
· 
Čtyři ortografické projekce
· 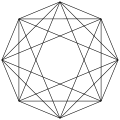
Šikmý ortogonální průmět uvnitř jeho pravidelného osmiúhelníkového Petrieho mnohoúhelníku, který spojuje všechny vrcholy kromě protilehlých.
· 
Šestnáctičlánek má dvě Wythoffovy konstrukce, pravidelnou formu a střídavou formu, které jsou zde znázorněny jako sítě, přičemž druhá forma je reprezentována střídavě dvěma barvami čtyřstěnových buněk.
· 
3D projekce 16-ti buněk provádějící dvojitou rotaci kolem dvou kolmých rovin.
Teselace
Čtyřrozměrný euklidovský prostor lze teselovat pravidelnými 16 buňkami. Tento systém se nazývá hexadekachorická včelí plástve a má Schläfliho symbol {3,3,4,3}. Duální tesselace, ikositetrachorická voština, {3,4,3,3}, je tvořena pravidelnými 24 buňkami. Spolu s teseraktickou voštinou {4,3,3,4} jsou to jediné tři pravidelné tesselace R4 . Každá 16-ti buňka má 16 sousedů, se kterými sdílí osmistěn, 24 sousedů, se kterými sdílí pouze hranu, a 72 sousedů, se kterými sdílí pouze jeden bod. Dvacet čtyři šestnáctičlánků se v této tesselaci setkává v libovolném vrcholu.
Projekce
První rovnoběžný průmět 16-ti buněk do 3-prostoru má krychlovou obálku. Nejbližší a nejvzdálenější buňky se promítají do vepsaných čtyřstěnů v krychli, což odpovídá dvěma možným způsobům vepsání pravidelného čtyřstěnu do krychle. Kolem každého z těchto čtyřstěnů jsou 4 další (nepravidelné) čtyřstěnné objemy, které jsou obrazy 4 okolních čtyřstěnových buněk a vyplňují prostor mezi vepsaným čtyřstěnem a krychlí. Zbývajících 6 buněk se promítá na čtvercové stěny krychle. V této projekci 16-ti buněk leží všechny její hrany na stěnách krychlového obalu.
Perspektivní projekce 16-ti buněk do 3-prostoru má trojstěnnou obálku. Uspořádání buněk v této obálce je analogické s uspořádáním buněk v rovnoběžném promítání.
Vrcholově první rovnoběžný průmět 16-ti buněk do 3-prostoru má osmistěnný obal. Tento osmistěn lze řezem podél souřadnicových rovin rozdělit na 8 čtyřstěnových objemů. Každý z těchto objemů je obrazem dvojice buněk 16-úhelníku. Nejbližší vrchol 16-úhelníku k pozorovateli se promítá do středu osmistěnu.
Nakonec má rovnoběžná projekce na hraně zkrácený osmistěnný obal a rovnoběžná projekce na čele má hexagonální bipyramidální obal.
Související stránky
- 24 buněk
- Polychoron
Vyhledávání