Vlnovec
Vlnovec je vložné zařízení z fyziky vysokých energií, které je obvykle součástí většího zařízení, synchrotronového úložného prstence. Skládá se z periodické struktury dipólových magnetů. Podél délky undulátoru se střídá statické magnetické pole o vlnové délce λ u {\displaystyle \lambda _{u}}. 
. Elektrony procházející periodickou strukturou magnetů jsou nuceny procházet oscilacemi. Elektrony tedy odevzdávají energii jako elektronmagnetické záření. Záření produkované v undulátoru je velmi intenzivní a koncentrované v úzkých energetických pásmech spektra. Světelný paprsek je navíc kolimován v rovině oběžné dráhy elektronů. Toto záření je vedeno paprskovými linkami pro experimenty v různých vědeckých oblastech.
Důležitý bezrozměrný parametr
K = e B λ u 2 π β m e c {\displaystyle K={\frac {eB\lambda _{u}}{2\pi \beta m_{e}c}}}} 
kde e je náboj částice, B je magnetické pole, β = v / c {\displaystyle \beta =v/c}
, m e {\displaystyle m_{e}}
je klidová hmotnost elektronu a c je rychlost světla, charakterizuje povahu pohybu elektronu. Pro K ≪ 1 {\displaystyle K\ll 1}
je amplituda oscilací pohybu malá a záření vykazuje interferenční vzorce, které vedou k úzkým energetickým pásům. Pokud je K ≫ 1 {\displaystyle K\gg 1}
, je amplituda kmitů větší a příspěvky záření z každé periody pole se sčítají nezávisle, což vede k širokému energetickému spektru. Je-li K mnohem větší než 1, zařízení se již nenazývá undulátor; nazývá se wiggler.
Fyzikové uvažují o vlnovkách jak pomocí klasické fyziky, tak pomocí teorie relativity. To znamená, že i když je přesný výpočet zdlouhavý, undulátor lze považovat za černou skříňku. Do této skříňky vstupuje elektron a malou výstupní štěrbinou z ní vychází elektromagnetický impuls. Štěrbina by měla být dostatečně malá, aby jí procházel pouze hlavní kužel, takže postranní laloky lze ignorovat.
Podvolníky mohou poskytnout stokrát větší magnetický tok než jednoduchý ohybový magnet, a proto jsou velmi žádané v zařízeních pro synchrotronové záření. U undulátoru, který se Nkrát opakuje (N period), může být jas až o N 2 {\displaystyle N^{2}}
větší než u ohybového magnetu. Intenzita se zvýší až na faktor N u harmonických vlnových délek v důsledku konstruktivní interference polí emitovaných během N period záření. Obvyklý impuls je sinusovka s určitou obálkou. Druhý činitel N pochází ze zmenšení vyzařovacího úhlu spojeného s těmito harmonickými, který se zmenšuje úměrně 1/N. Když elektrony přicházejí s poloviční periodou, interferují destruktivně. Vlnovec tedy zůstává temný. Totéž platí, pokud elektrony přicházejí jako korálkový řetězec. Protože se svazek elektronů rozprostře tím vícekrát, čím více cestuje kolem synchrotronu, chtějí fyzikové navrhnout nové přístroje, které svazky elektronů vyhodí dříve, než se stihnou rozprostřít. Díky této změně vznikne užitečnější synchrotronové záření.
Polarizaci vyzařovaného záření lze řídit pomocí permanentních magnetů, které indukují různé periodické trajektorie elektronů v undulátoru. Pokud jsou oscilace omezeny na rovinu, bude záření lineárně polarizované. Pokud je trajektorie oscilací šroubovicová, bude záření polarizováno kruhově, přičemž ručička je určena šroubovicí.
Pokud se elektrony řídí Poissonovým rozdělením, vede částečná interference k lineárnímu nárůstu intenzity. V laseru svolnými elektrony roste intenzita exponenciálně s počtem elektronů.
Fyzikové měří účinnost vlnolamu pomocí spektrálního záření.
Vícepólový wiggler, který se používá v akumulačním prstenci na australském synchrotronu pro generování synchrotronového záření.
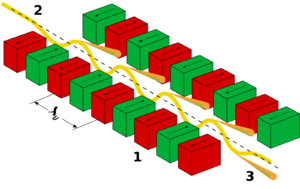
Fungování vlnovce. 1: magnety, 2: elektronový svazek, 3: synchrotronové záření.
Historie
První undulátor sestrojil Hans Motz se svými spolupracovníky na Stanfordu v roce 1953. Jeden z jejich undulátorů produkoval vůbec první koherentní infračervené záření. Jejich celkový frekvenční rozsah byl od viditelného světla až po milimetrové vlny. Ruský fyzik V. L. Ginzburg ve své práci z roku 1947 ukázal, že undulátory lze v principu vyrobit.
Otázky a odpovědi
Otázka: Co je to vlnovka?
Odpověď: Undulátor je zařízení z fyziky vysokých energií, které se skládá z periodické struktury dipólových magnetů. Nutí elektrony podstupovat oscilace, které produkují intenzivní a koncentrované elektromagnetické záření v úzkých energetických pásmech.
Otázka: Jaký parametr charakterizuje povahu pohybu elektronů?
Odpověď: Charakter pohybu elektronů charakterizuje důležitý bezrozměrný parametr K = eBλu/2πβmecc, kde e je náboj částice, B je magnetické pole, β = v/c , me je klidová hmotnost elektronu a c je rychlost světla.
Otázka: Jak je na tom undulátor v porovnání s ohýbacím magnetem z hlediska magnetického toku?
Odpověď: Podvolníky mohou poskytnout stokrát větší magnetický tok než jednoduchý ohybový magnet.
Otázka: Jak ovlivňuje interference intenzitu při použití undulátoru?
Odpověď: Je-li K ≤ 1, pak je amplituda kmitů malá a záření vykazuje interferenční vzorce, které vedou k úzkým energetickým pásům. Pokud je K ≥ 1, pak je amplituda oscilací větší a příspěvky záření z každé periody pole se sčítají nezávisle, což vede k širokému energetickému spektru.
Otázka: Jak lze řídit polarizaci při použití undulátoru?
Odpověď: Polarizaci lze řídit pomocí permanentních magnetů, které indukují různé periodické trajektorie elektronů v undulátoru. Pokud jsou oscilace omezeny na rovinu, bude záření lineárně polarizované; pokud je trajektorie šroubovicová, bude záření kruhově polarizované s ručičkami určenými šroubovicí.
Otázka: Jak roste intenzita s počtem elektronů u laserů na volných elektronech?
Odpověď: Pokud se elektrony řídí Poissonovým rozdělením, vede částečná interference k lineárnímu nárůstu intenzity; u laserů na volných elektronech roste intenzita exponenciálně s počtem elektronů.
Otázka: Jaké měřítko používají fyzikové k vyhodnocení účinnosti undulátoru?
Odpověď: Fyzikové měří účinnost undulátoru pomocí spektrálního záření.
